Dominant/Co-Dominant Genetics
Let's start simple. Say we have a Pastel and want to breed it to a normal. We need to
label each snake in terms of the genes involved, whether they have the trait or not.
We'll call the Pastel gene "P" and the normal gene "p," so the Pastel will be labeled
Pp and the normal pp (normal is dominant). This is the main step where people get
confused, so this is important to understand. Why do we use pp for the normal instead of
NN? It really doesn't matter all that much for this example, but once we get to more
complex crosses, it will become very important. Just go with it for now. :-]
Okay, so we're breeding Pp with pp.
We use Punnett squares (named after some dude who came up with them) to make this easier.
(If you're not a visually-oriented person, maybe this won't make things easier.)
Remember, each parent only passes on one gene, so the first parent can pass P or p and
the second parent can pass p or p. (Yes, you need to keep track of everything, including
duplicates.) Let's put parent 1 along the top and parent 2 along the left, like so:
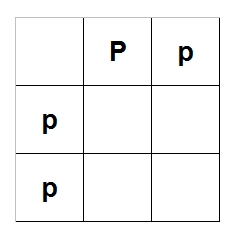
Now, fill in the rest of the chart by combining letters from each column and row, like this:
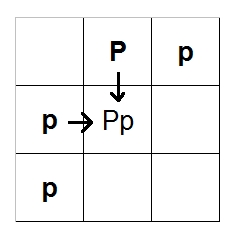
When you're done, it should look like this:
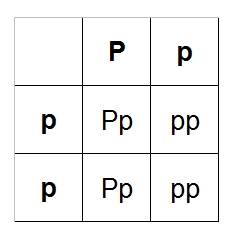
The four boxes we just filled in are possible offspring: Pp, Pp, pp, pp. Remember that the
Pastel gene is co-dom, so anything with only one P will be a Pastel. Out of our four possible
offspring, two of them are pastels (Pp, Pp) and two are normals (pp, pp). Two out of four
will be Pastels, and two out of four will be normal. Two out of four = 2/4 = 1/2 = 50%.
This means that for each egg, you have a 50% chance of getting a Pastel or a normal.
Remember that these are probabilities only; it doesn't mean you will always get half Pastels
and half normals. You could get one Pastel and the rest normals or vice versa. It's a
coin toss for each egg.
End of simple example. Make sense? Yes? Okay, on to something a little more complex.
A favorite combo snake among ball python enthusiasts is the Pastel Spider, also known as a
Bumblebee. The simplest way to get a Bumblebee is to cross a Pastel with a Spider.
In the above example, we used Pp to denote a Pastel. Since Spiders are also co-dom, we
can do the same thing (but use a different letter); let's call our Spider Ss.
So we have Pp x Ss. Each parent passes on one gene for each trait, so Parent 1 can pass on "P" or
"p," and Parent 2 can pass on "S" or "s." Put the parents along the top and left like last time:
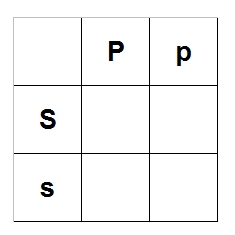
Now fill in the empty parts of the chart the same way as last time:
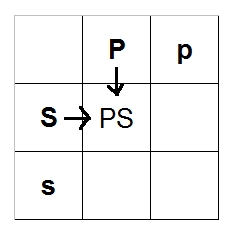
You should end up with this:
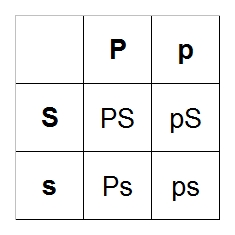
Again, we have four possibilities: PS, Ps, pS, ps. We're still dealing with dom/co-dom traits,
so the lower-case letters basically mean "normal."
PS = Pastel Spider (Bumblebee)
Ps = Pastel
pS = Spider
ps = Normal
So one out of four can be a Bumblebee: 1/4 = 25%
Same goes for the Pastel, Spider, and normal, so each egg has a 25% chance of being a Bumblebee,
Pastel, Spider, or a normal.
Now, technically, this Bumblebee example was greatly simplified. What we should have done is
include both the Spider and Pastel genes for each snake. In other words, we need to account
for both Spider and Pastel genes even if they aren't actually there. For example, a Spider
could be written ppSs instead of just Ss. (You could write it Ssfoofoo if you want, but
since we're dealing with Spiders and Pastels, let's keep it as simple as possible and only
include Spider and Pastel genes.) Same goes for the Pastel: Ppss instead of Pp. I know
it seems like we're making it more complicated than it needs to be, but it is absolutely
necessary, which I will show soon.
Let's do our Pastel x Spider again, this time with all genes: Ppss x ppSs. Now, each parent
can pass on one gene of each trait. So Snake 1 can pass on Ps, Ps, ps, ps. Snake 2
can pass on pS, ps, pS, ps. This will give us a 4x4 chart instead of a 2x2; put the Snake 1
possibilities along the top and Snake 2 along the left-hand side, just like before:
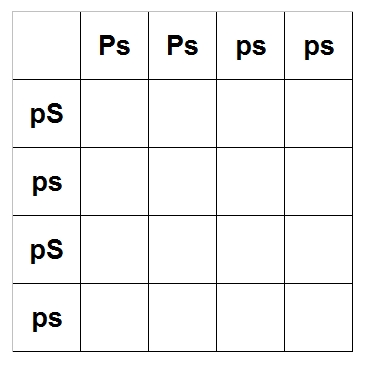
Now, start to fill in the chart the same way as last time:
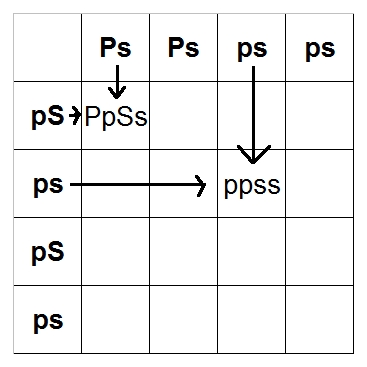
When you're done, it should look like this:
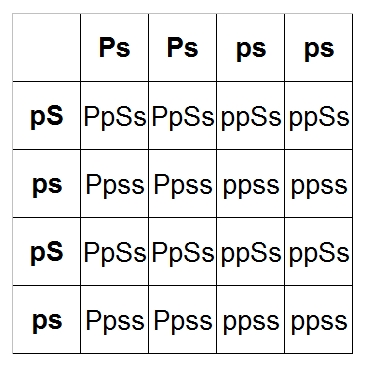
Don't panic! This isn't as complex as it looks! Remember we only need one Pastel gene (P) to get
a Pastel and only one Spider gene (S) to get a Spider, so anything with a capital P is a Pastel
and anything with a capital S is a Spider. Therefore,
PpSs = Pastel Spider (Bumblebee)
Ppss = Pastel
ppSs = Spider
ppss = Normal
We have 16 possible combinations of offspring. Let's count up the number of Bumblebees (PpSs):
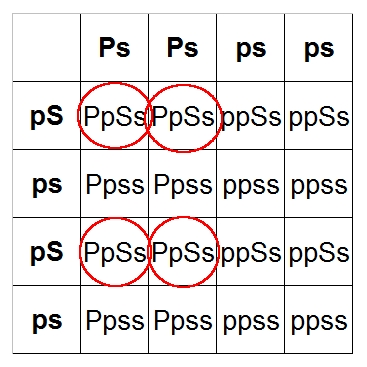
We have four out of 16 = 4/16 = 1/4 = 25% See? Same as last time! Yay! Count up the number
of Pastels, Spiders, and normals, and they all come out to be 25%.
So why the crap would we do it that way instead of the previous, easier way? We'll answer that
question by crossing a Bumblebee with a normal!
Remember to include all genes, so the Bumblebee will be PpSs and a normal will be ppss.
The Bumblebee can pass PS, Ps, pS, ps and the normal can pass ps, ps, ps, ps.
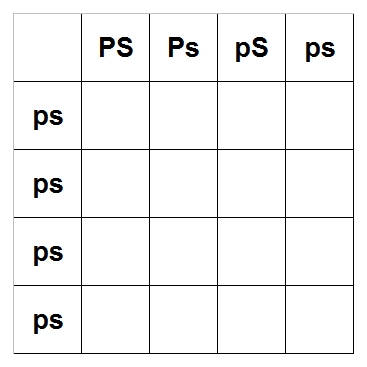
Fill it in like all the other times. The double-quote means that box is the same as the one
above it.
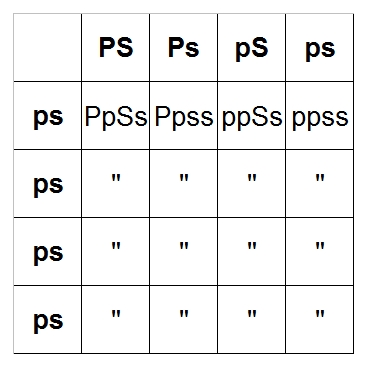
PpSs = Pastel Spider (Bumblebee) = 4/16 = 25%
Ppss = Pastel = 4/16 = 25%
ppSs = Spider = 4/16 = 25%
ppss = Normal = 4/16 = 25%
Isn't that interesting? We get the same possibilities crossing a Bumblebee with a normal as
crossing a Pastel with a Spider! This is very useful information. If you want to make a
Bumblebee as cheaply as possible, you
can buy a Pastel and cross it with a Spider, but if you want to make as many Bumblebees as
possible, you can get a male Bumblebee (cheaper than a female Bumblebee) and a lot of normal
females. This is a great example of why it's important for a breeder to be able to do
Punnett squares: it will help you decide what you need to breed to get what you want,
whether that be as many morphs as possible, as cheaply as possible, or whatever.
Okay, time to really blow your noggin'. Let's try a Killerbee (Super Pastel Spider) crossed
with a Spinner Blast (Pastel Spider Pinstripe)!
Pastel = Pp
Super Pastel = PP
Spider = Ss
Pinstripe = Nn
Killerbee = PPSsnn
Spinner Blast = PpSsNn
Killerbee combinations: PSn, PSn, Psn, Psn, PSn, PSn, Psn, Psn
Spinner Blast combinations: PSN, PSn, PsN, Psn, pSN, pSn, psN, psn
I'm going to make it easier and put the Spinner Blast on the top and the Killerbee on the left,
but it doesn't really matter. The matrix should be 8x8, but I
shortened it to an 8x2 because there are only two unique Killerbee combinations. We can't
just ignore the duplicates, so I've added "4x" in front of each row that repeats four times.
That means when I start calculating probabilities at the end, each probability in a row
with "4x" needs to be multiplied by 4.
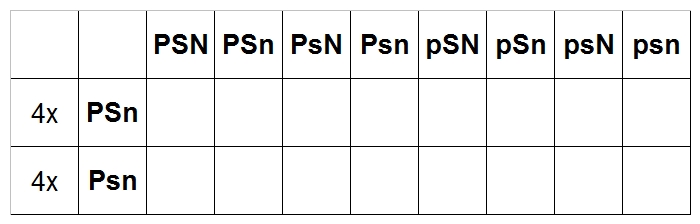
And we fill it out....
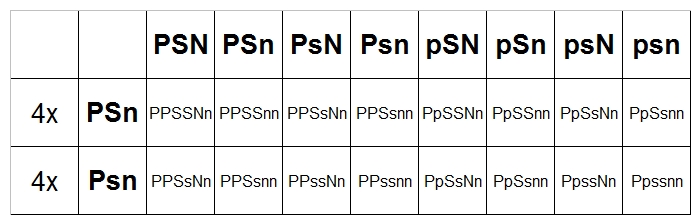
Now, remember that Spiders and Pinstripes are Dominant, so Ss is the same as SS and Nn is the same
as NN.
PPSSNn = PPSsNn = Super Pastel Spider Pinstripe = 12/64 = 3/16 = 18.75%
PPSSnn = PPSsnn = Super Pastel Spider (Killerbee) = 12/64 = 3/16 = 18.75%
PPssNn = Super Pastel Pinstripe (Super Blast) = 4/64 = 1/16 = 6.25%
PPssnn = Super Pastel = 4/64 = 1/16 = 6.25%
PpSSNn = PpSsNn = Pastel Spider Pinstripe (Spinner Blast) = 12/64 = 3/16 = 18.75%
PpSSnn = PpSsnn = Pastel Spider (Bumblebee) = 12/64 = 3/16 = 18.75%
PpssNn = Pastel Pinstripe (Lemon Blast) = 4/64 = 1/16 = 6.25%
Ppssnn = Pastel = 4/64 = 1/16 = 6.25%
Whew! What a doozy! Best to double-check your calculations in a case like this: all fractions
should add up to 1 and all percentages should add up to 100.
|